Маятник Капицы

Одна из конструкция маятника Капицы: мотор приводит кривошип, который через шатун и рычаг передаёт вибрацию на перевёрнутый маятник.

Ма́ятником Капицы называется система, состоящая из грузика, прикрепленного к легкой нерастяжимой спице, которая крепится к вибрирующему подвесу. Маятник носит имя академика и нобелевского лауреата П. Л. Капицы, построившего в 1951 г. теорию для описания такой системы ^[1]. При неподвижной точке подвеса, модель описывает обычный математический маятник, для которого имеются два положения равновесия: в нижней точке и в верхней точке. При этом равновесие математического маятника в верхней точке является неустойчивым, и любое сколь угодно малое возмущение приводит к потере равновесия.

Удивительной особенностью маятника Капицы является то, что вопреки интуиции перевернутое (вертикальное) положение маятника может быть устойчивым в случае быстрых вибраций подвеса. Хотя такое наблюдение было сделано еще в 1908 г. А. Стефенсоном^[2], в течение длительного времени не имелось математического объяснения причин такой устойчивости. П. Л. Капица экспериментально исследовал такой маятник, а также построил теорию динамической стабилизации, разделяя движение на «быстрые» и «медленные» переменные и введя эффективный потенциал. Работа П. Л. Капицы, опубликованная в 1951 году^[1], открыла новое направление в физике — вибрационную механику. Метод П. Л. Капицы используется для описания колебательных процессов в атомной физике, физике плазмы, кибернетической физике. Эффективный потенциал, описывающий «медленную составляющую движения», описывается в томе «механика» курса теоретической физики Л. Д. Ландау^[3].

Маятник Капицы интересен еще и тем, что в такой простой системе можно наблюдать параметрические резонансы, когда нижнее положение равновесия не является больше устойчивым и амплитуда малых отклонений маятника нарастает со временем^[4]. Также, при большой амплитуде вынуждающих колебаний в системе могут реализовываться хаотические режимы, когда в сечении Пуанкаре наблюдаются странные аттракторы.

Обозначения

Схема маятника Капицы

Направим ось $y$ вертикально вверх, а ось $x$ горизонтально, так чтобы плоское движение маятника происходило в плоскости ($x$ — $y$). Введем обозначения:

• $\nu$ — частота вынуждающих вертикальных гармонических колебаний подвеса,
• $a$ — амплитуда вынуждающих колебаний,
• $\omega_0 = \sqrt{g/l}$ — собственная частота колебаний математического маятника,
• $g$ — ускорение свободного падения,
• $l$ — длина легкого стержня,
• $m$ — масса грузика.

Если угол между стержнем и осью $y$ обозначить как $\varphi$, то зависимость координат грузика от времени запишется следующими формулами:

$\begin{matrix} \left\{ \begin{matrix} x &=& l \sin \varphi\\ y &=& - l \cos \varphi - a \cos \nu t \end{matrix} \right. \end{matrix}$

Энергия маятника

Потенциальная энергия маятника в поле тяжести задается положением грузика по вертикали как

$\begin{matrix} E_{POT} = - m g (l \cos \varphi + a \cos \nu t)\;. \end{matrix}$

В кинетической энергии помимо обычного слагаемого $E_{KIN}=m l^2 \dot \varphi^2 /2$, описывающего движение математического маятника, имеются дополнительные составляющие, вызванные вибрацией подвеса:

$\begin{matrix} E_{KIN} = \frac{m l^2 }{2} \dot \varphi^2 + m a l \nu ~\sin(\nu t) \sin(\varphi)~\dot\varphi + \frac{m a^2 \nu^2}{2} \sin^2(\nu t)\;. \end{matrix}$

Полная энергия дается суммой кинетической и потенциальной энергий $E = E_{KIN} + E_{POT}$, а лагранжиан системы их разностью $L = E_{KIN} - E_{POT}$.

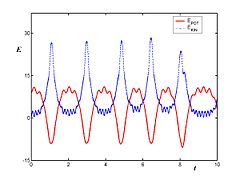
Для математического маятника полная энергия является сохраняющейся величиной, поэтому кинетическая энергия $E_{KIN}$ и потенциальная энергия $E_{POT}$ на графике их зависимости от времени $t$ симметричны относительно горизонтальной прямой. Из теоремы вириала следует, что средняя кинетическая и потенциальная энергии в гармоническом осцилляторе равны. Поэтому горизонтальная прямая, относительно которой имеется симметрия $E_{KIN}$ и $E_{POT}$, соответствует половине полной энергии.

Характерные зависимости потенциальной и кинетической энергий от времени для математического маятника

Если подвес колеблется, то полная энергия больше не сохраняется. Кинетическая энергия является более чувствительной к вынуждающим колебаниям, чем потенциальная. Потенциальная энергия $E_{POT} = mgy$ ограничена как сверху, так и снизу $-mg(l+a)<E_{POT}<mg(l+a)$, в то время как кинетическая энергия ограничена только снизу $E_{KIN}\ge 0$. При больших значениях частоты $\nu$, кинетическая энергия может быть много больше потенциальной.

Характерные зависимости потенциальной и кинетической энергий от времени для маятника Капицы

Уравнение движения

Движение маятника удовлетворяет уравнениям Эйлера — Лагранжа. Зависимость фазы маятника $\varphi$ от времени определяет положение грузика^[5]:

$\begin{matrix} \frac{d}{dt} \frac{\partial L}{\partial \dot \varphi} = \frac{\partial L}{\partial \varphi}\;. \end{matrix}$

Дифференциальное уравнение, описывающие эволюцию фазы маятника

$\begin{matrix} \ddot \varphi = - (a~\nu^2\cos\nu t~ +g) \frac{\sin \varphi}{l}\;, \end{matrix}$

нелинейно из-за имеющегося в нем множителя $\sin\varphi$. Наличие нелинейного слагаемого может приводить к хаотическому поведению и появлению странных аттракторов.

Положения равновесия

Колебания маятника Капицы в глобальном (нижнем) минимуме.

Модель маятника Капицы является более общей, чем модель математического маятника. Последняя получается в предельном случае $a = 0$. Фазовый портрет математического маятника хорошо известен. На координатной плоскости это просто окружность $x^2+y^2 = l^2 = const$. Если в начальный момент времени энергия маятника была больше, чем максимум потенциальной энергии $E > mgl$, то траектория будет замкнутой и циклической. Если же энергия маятника была меньше $E < mgl$, то он будет совершать периодические колебания около единственной устойчивой точки равновесия с наименьшим значением потенциальной энергии $x = 0,~y = -l$. В случае математического маятника полная энергии системы не меняется.

Колебания маятника Капицы в в локальном (верхнем) минимуме.

В случае $a \ne 0$ система более не является замкнутой и ее полная энергия может изменяться. Если при этом, частота вынуждающих колебаний $\nu$ много больше частоты собственных колебаний $\omega_0$, то такой случай можно проанализировать математически. Оказывается^[1], что если ввести эффективный потенциал, в котором движется маятник (медленно относительно частоты $\nu$), то этот потенциал может иметь два локальных минимума — один, как и раньше в нижней точке $(0,-l)$, а другой в верхней точке $(0,l)$. То есть точка $(0,l)$ абсолютно неустойчивого равновесия для математического маятника, может оказаться точкой устойчивого равновесия для маятника Капицы.

Фазовый портрет

Портрет системы в координатном пространстве для маятника Капицы при относительно небольшой амплитуде вынуждающих колебаний

Интересные фазовые портреты могут быть получены для значений параметров, недоступных для аналитического рассмотрения, например в случае большой амплитуды колебания подвеса $a \approx l$^[6][7]. Если увеличить амплитуду вынуждающих колебаний до половины длины маятника $a = l/2$, то получится картина аналогичная той, которая изображена на рисунке.

Портрет системы в координатном пространстве для маятника Капицы при большой амплитуде вынуждающих колебаний

При дальнейшем увеличении амплитуды $a$ (начиная от значения $a = l$), все внутреннее пространство начинает «замазываться» полностью, то есть, если ранее не все внутренние точки координатного пространства были доступны, то теперь система может побывать в любой точке. Очевидно, что дальнейшее увеличение длины $a$ принципиально более не изменит картину.

Интересные факты

• Как отмечал П. Л. Капица, маятниковые часы на вибрирующем основании всегда спешат.
• В коридоре института физических проблем стояла работающая модель маятника Капицы, и любой желающий мог воочию убедиться, как при ее включении маятник поднимался и оставался в вертикальном положении.
• Метод эффективного потенциала был разработан П. Л. Капицей во время работы над высокочастотным генератором «ниготроном», названным так по месту исследования у себя на даче на Николиной Горе. Для того чтобы не было проблем с «секретностью» при публикации метода, П. Л. Капица придумывает простую физическую модель, к которой был бы применим этот метод. Таким образом, появляются статьи^[1] про маятник с вибрирующим подвесом.
• П. Л. Капица предлагал решить задачу в измененном варианте поступающим к нему в аспирантуру. Требовалась отыскать условие устойчивости акробата на доске, положенной на цилиндр, лежащий на боку. Ожидаемый ответ был, что если акробат начинал быстро переступать ногами, то его положение становилось устойчивым.
• При ходьбе устойчивость тела увеличивается в несколько раз по сравнению с устойчивостью при стоянии. Этот биомеханический феномен до настоящего времени не изучен. Существует гипотеза, которая объясняет устойчивость тела при ходьбе колебательными движениями центра голеностопного сустава. Тело человека представляется с позиции перевернутого маятника с центром в области голеностопных суставов, который приобретает устойчивость в вертикальном положении, если его центр совершает колебание вверх-вниз с достаточно высокой частотой (маятник Капицы).

Литература

1. ↑ ^{1 2 3 4} Капица П. Л. «Динамическая устойчивость маятника при колеблющейся точке подвеса» ЖЭТФ, т. 21, вып. 5. с. 588—597 (1951); Капица П. Л. «Маятник с вибрирующим подвесом», УФН, т. 44. Вып. 1. С. 7-20 (1951).
2. ↑ A. Stephenson «On an induced stability» Phil. Mag. 15, 233 (1908)
3. ↑ Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6
4. ↑ Бутиков Е. И. «Маятник с осциллирующим подвесом (к 60-летию маятника Капицы»), учебное пособие.
5. ↑ Крайнов В. П. Избранные математические методы в теоретической физике. Издательство МФТИ (1996).
6. ↑ Астрахарчик Г.Е и Астрахарчик Н. А. «Исследование маятника Капицы» (G.E. Astrakharchik, N.A. Astrakharchik «Numerical study of Kapitza pendulum») arXiv:1103.5981 (2011)
7. ↑ Визуализация в реальном времени движений маятника Капицы доступна в интернете на сайтах http://www.myphysicslab.com/beta/Inverted-pendulum.html и http://faculty.ifmo.ru/butikov/Nonlinear/index.html Параметры маятника могут быть выбраны произвольно и вводятся вручную.